Formulation du problème
Étant donné un nombre entier n .
Obtenir tous les diviseurs c du nombre n de sorte que c * i = n pour un autre entier i . Le format de sortie souhaité est une liste d'entiers (diviseurs).
Voici quelques exemples :
n = 10 # Output: [1, 2, 5, 10] n = 13 # Output: [1, 13] n = 24 # Output: [1, 2, 3, 4, 6, 8, 12]
Méthode 1 :Approche naïve
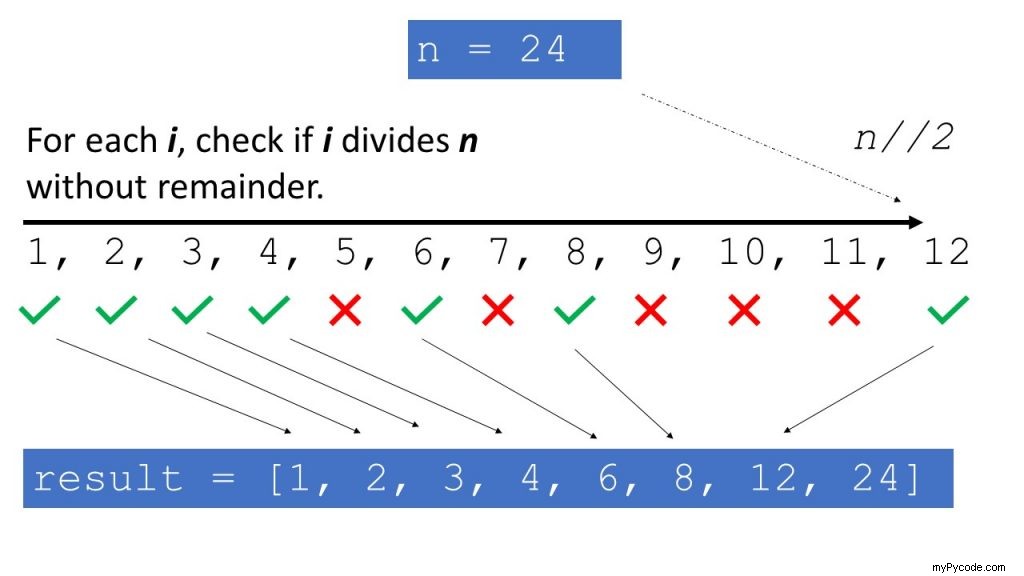
Entier i est un diviseur de n si n modulo i est zéro.
Nous utilisons cette observation dans la fonction divisors() . On crée une liste initialement vide result et vérifie chaque nombre entier i entre 0 et n/2 si ce nombre est un diviseur de n . Si c'est le cas, nous l'ajoutons à la liste.
Le code Python suivant accomplit cela :
def divisors(n):
result = []
for i in range(1, n//2 + 1):
if n % i == 0:
result.append(i)
result.append(n)
return result
print(divisors(24))
# [1, 2, 3, 4, 6, 8, 12, 24]
Cette approche n'est pas très efficace car nous parcourons chaque nombre de 0 à n/2 . Si le nombre n devient grand tel que n=1000000 , nous devons vérifier chaque nombre i=0, i=1, i=2, i=3, ..., i=500000 .
Complexité d'exécution : La complexité d'exécution du calcul des diviseurs du nombre n est O(n) en utilisant cette approche en supposant que l'opération modulo peut être effectuée en une seule étape.
Peut-on faire mieux ? Oui !
Méthode 2 :réduction du nombre d'itérations de boucle
Nous utilisons deux observations pour réduire le nombre d'itérations de boucle de "l'algorithme naïf".
Observation 1 : Si numéro i est un diviseur de n , numéro j = n/i doit être un entier et un diviseur de n aussi parce que i * n/i = n . Cela signifie qu'à chaque fois que l'on trouve un diviseur i , on peut aussi ajouter le diviseur n/i à la liste des diviseurs.
Observation 2 : Pour une paire de n -diviseurs (i, j) , l'un d'eux doit être inférieur ou égal à la racine carrée de n . La raison est simple :si les deux étaient supérieurs à la racine carrée, la multiplication i * j serait supérieur à n bien sûr parce que root(n) * root(n) == n . Ainsi, nous pouvons parcourir les diviseurs potentiels à partir de i=0 à i=root(n) et assurez-vous d'avoir trouvé tous les diviseurs. Cela nous évite toutes les itérations de i=root(n) à i=n//2 .
Voici le réglage simple avec des avantages significatifs en termes de performances :
def divisors(n):
result = set()
for i in range(1, int(n**0.5)+1):
if n % i == 0:
result.add(i)
result.add(n//i)
return list(result)
print(divisors(24))
# [1, 2, 3, 4, 6, 8, 12, 24]
Ce code itère uniquement de 0 à la racine carrée du nombre n . Si on trouve un diviseur i , nous ajoutons également n//i qui est l'autre facteur et un diviseur de n aussi bien.
Complexité d'exécution : La complexité d'exécution du calcul des diviseurs du nombre n est O(n^0.5) en utilisant cette approche en supposant que l'opération modulo est comptée comme une étape.
Humour de programmeur – Blockchain