Présentation
Le calcul des nombres premiers à partir d'une série de nombres donnée n'est peut-être pas un gros problème. Cependant, le calcul des nombres premiers de la manière la plus efficace en gardant à l'esprit la complexité temporelle et d'autres facteurs peut être un problème difficile. Après tout, l'un des critères majeurs d'un code efficace est son efficacité. Par conséquent, dans cet article, nous allons comparer et contraster les complexités de différents codes pour calculer tous les nombres premiers inférieurs à N , où N désigne un nombre arbitraire de valeurs dans la série donnée telle qu'entrée par l'utilisateur.
Exemple : Vous trouverez ci-dessous un exemple simple de ce qui va suivre dans cet article :
import time
start_time = time.time()
n = int(input("Enter the last range of the series: "))
for i in range(1,n+1):
if i>1:
for j in range(2,i):
if(i % j==0):
break
else:
print(i)
end_time = time.time()
print("Elapsed Time: " + str(end_time-start_time)) Sortie :
Enter the last range of the series: 10 2 3 5 7 Elapsed Time: 3.9661035537719727
❖ Avertissement : Les méthodes utilisées dans le script ci-dessous sont purement basées sur le moins de temps nécessaire pour calculer les nombres premiers
Sans plus tarder, plongeons-nous dans les comparaisons et visualisons le résultat.
Au lieu de comparer les codes un par un ce qui allongerait inutilement l'article, voici une liste de toutes les méthodes probables pour calculer des nombres premiers dans une plage donnée avec le moins de temps de calcul possible.
Sortie :
D'après l'analyse ci-dessus, il est clair que la Méthode 3 prend le minimum temps pour calculer les nombres premiers
Notre gagnant :Méthode 3
❖ Avis de non-responsabilité : Les valeurs du temps écoulé pris par chaque méthode telles que calculées par le
Si vous utilisez toujours Python 2.x, vous pourriez avoir envie des méthodes suivantes indiquées ci-dessous :
Sortie :
Considérant que l'extrait ci-dessus est écrit dans un fichier avec le nom plot.py , voici une analyse graphique des temps mis par chaque méthode pour calculer tous les nombres premiers inférieurs à N. Le code ci-dessous est utilisé pour tracer le bar-graph pour comparer les différentes méthodes utilisées pour calculer les nombres premiers
Tracé/Graphique Sortie :
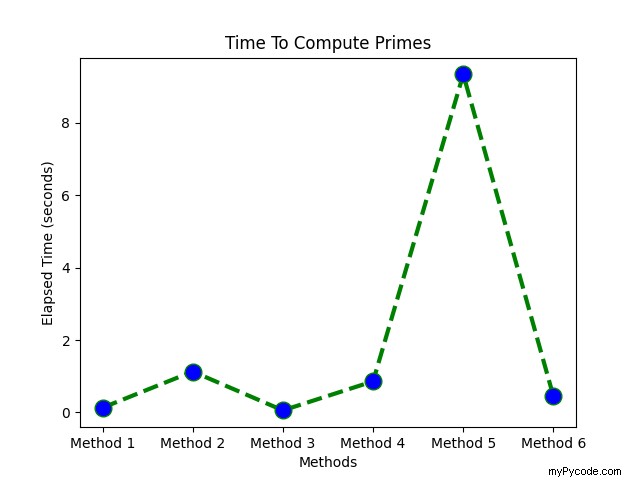
❖ Vous trouverez ci-dessous une autre comparaison graphique utilisant un graphique linéaire en pointillés qui compare le temps pris par chaque méthode :
Sortie :
Le code pour générer le graphique ci-dessus est donné ci-dessous (Le code contenant les principales méthodes a été mentionné ci-dessus. Nous considérons qu'il est présent dans un fichier plot.py, puis nous l'importons dans notre fichier de classe principal pour tracer le graphique.)
Dans cet article, nous avons comparé plusieurs méthodes et trouvé la meilleure méthode en termes de temps minimum nécessaire pour calculer tous les nombres premiers
J'espère que vous avez apprécié l'article, veuillez vous abonner et rester à l'écoute pour des articles et des contenus plus intéressants comme celui-ci.
Référence : https://stackoverflow.com/questions/2068372/fastest-way-to-list-all-primes-below-nComparaison de codes
from sympy import sieve
import numpy
import itertools
izip = itertools.zip_longest
chain = itertools.chain.from_iterable
compress = itertools.compress
import time
def method1(n):
""" Returns a list of primes < n """
sieve = [True] * n
for i in range(3, int(n ** 0.5) + 1, 2):
if sieve[i]:
sieve[i * i::2 * i] = [False] * ((n - i * i - 1) // (2 * i) + 1)
return [2] + [i for i in range(3, n, 2) if sieve[i]]
def method2(n):
""" Returns a list of primes < n """
sieve = [True] * (n // 2)
for i in range(3, int(n ** 0.5) + 1, 2):
if sieve[i // 2]:
sieve[i * i // 2::i] = [False] * ((n - i * i - 1) // (2 * i) + 1)
return [2] + [2 * i + 1 for i in range(1, n // 2) if sieve[i]]
def method3(n):
""" Input n>=6, Returns a array of primes, 2 <= p < n """
sieve = numpy.ones(n // 3 + (n % 6 == 2), dtype=numpy.bool)
for i in range(1, int(n ** 0.5) // 3 + 1):
if sieve[i]:
k = 3 * i + 1 | 1
sieve[k * k // 3::2 * k] = False
sieve[k * (k - 2 * (i & 1) + 4) // 3::2 * k] = False
return numpy.r_[2, 3, ((3 * numpy.nonzero(sieve)[0][1:] + 1) | 1)]
def method4(n):
""" Input n>=6, Returns a list of primes, 2 <= p < n """
n, correction = n - n % 6 + 6, 2 - (n % 6 > 1)
sieve = [True] * (n // 3)
for i in range(1, int(n ** 0.5) // 3 + 1):
if sieve[i]:
k = 3 * i + 1 | 1
sieve[k * k // 3::2 * k] = [False] * ((n // 6 - k * k // 6 - 1) // k + 1)
sieve[k * (k - 2 * (i & 1) + 4) // 3::2 * k] = [False] * (
(n // 6 - k * (k - 2 * (i & 1) + 4) // 6 - 1) // k + 1)
return [2, 3] + [3 * i + 1 | 1 for i in range(1, n // 3 - correction) if sieve[i]]
def method5(n):
primes = list(sieve.primerange(1, n))
return primes
def method6(n):
""" Input n>=6, Returns a list of primes, 2 <= p < n """
zero = bytearray([False])
size = n // 3 + (n % 6 == 2)
sieve = bytearray([True]) * size
sieve[0] = False
for i in range(int(n ** 0.5) // 3 + 1):
if sieve[i]:
k = 3 * i + 1 | 1
start = (k * k + 4 * k - 2 * k * (i & 1)) // 3
sieve[(k * k) // 3::2 * k] = zero * ((size - (k * k) // 3 - 1) // (2 * k) + 1)
sieve[start::2 * k] = zero * ((size - start - 1) // (2 * k) + 1)
ans = [2, 3]
poss = chain(izip(*[range(i, n, 6) for i in (1, 5)]))
ans.extend(compress(poss, sieve))
return ans
m1_start = time.time()
method1(10 ** 6)
m1_end = time.time()
m1_et = m1_end - m1_start
print("Method 1 Elapsed time: " + str(m1_end - m1_start))
m2_start = time.time()
method2(10 ** 7)
m2_end = time.time()
m2_et = m2_end - m2_start
print("Method 2 Elapsed time: " + str(m2_end - m2_start))
m3_start = time.time()
method3(10 ** 7)
m3_end = time.time()
m3_et = m3_end - m3_start
print("Method 3 Elapsed time: " + str(m3_end - m3_start))
m4_start = time.time()
method4(10 ** 7)
m4_end = time.time()
m4_et = m4_end - m4_start
print("Method 4 Elapsed time: " + str(m4_end - m4_start))
m5_start = time.time()
method5(10 ** 7)
m5_end = time.time()
m5_et = m5_end - m5_start
print("Method 5 Elapsed time: " + str(m5_end - m5_start))
m6_start = time.time()
method6(10 ** 7)
m6_end = time.time()
m6_et = m6_end - m6_start
print("Method 6 Elapsed time: " + str(m6_end - m6_start))
Method 1 Elapsed time: 0.06881570816040039
Method 2 Elapsed time: 0.9155552387237549
Method 3 Elapsed time: 0.045876264572143555
Method 4 Elapsed time: 0.6512553691864014
Method 5 Elapsed time: 7.0082621574401855
Method 6 Elapsed time: 0.33211350440979004
time module peut varier en fonction du système/matériel utilisé et de la version de Python que vous utilisez.from math import sqrt
import time
def method1(max_n):
numbers = range(3, max_n + 1, 2)
half = (max_n) // 2
initial = 4
for step in range(3, max_n + 1, 2):
for i in range(initial, half, step):
numbers[i - 1] = 0
initial += 2 * (step + 1)
if initial > half:
return [2] + filter(None, numbers)
def method2(n):
"""sieveOfEratosthenes(n): return the list of the primes < n."""
if n <= 2:
return []
sieve = range(3, n, 2)
top = len(sieve)
for si in sieve:
if si:
bottom = (si * si - 3) // 2
if bottom >= top:
break
sieve[bottom::si] = [0] * -((bottom - top) // si)
return [2] + [el for el in sieve if el]
def method3(n):
s = range(3, n, 2)
for m in xrange(3, int(n ** 0.5) + 1, 2):
if s[(m - 3) / 2]:
for t in xrange((m * m - 3) / 2, (n >> 1) - 1, m):
s[t] = 0
return [2] + [t for t in s if t > 0]
def method4(size):
prime = [True] * size
rng = xrange
limit = int(sqrt(size))
for i in rng(3, limit + 1, +2):
if prime[i]:
prime[i * i::+i] = [False] * len(prime[i * i::+i])
return [2] + [i for i in rng(3, size, +2) if prime[i]]
m1_start = time.time()
method1(10 ** 6)
m1_end = time.time()
print("Method 1 Elapsed time: " + str(m1_end - m1_start))
m2_start = time.time()
method2(10 ** 6)
m2_end = time.time()
print("Method 2 Elapsed time: " + str(m2_end - m2_start))
m3_start = time.time()
method3(10 ** 6)
m3_end = time.time()
print("Method 3 Elapsed time: " + str(m3_end - m3_start))
m4_start = time.time()
method4(10 ** 6)
m4_end = time.time()
print("Method 4 Elapsed time: " + str(m4_end - m4_start)) Method 1 Elapsed time: 0.891271114349
Method 2 Elapsed time: 0.178880214691
Method 3 Elapsed time: 0.526117086411
Method 4 Elapsed time: 0.29536986351
Comparaison graphique
import plot
import matplotlib.pyplot as plt
import numpy as np
method = ['Method 1', 'Method 2', 'Method 3', 'Method 4', 'Method 5', 'Method 6']
et = [plot.m1_et, plot.m2_et, plot.m3_et, plot.m4_et, plot.m5_et, plot.m6_et]
c = ["red", "green", "orange", "blue", "black", "purple"]
ypos = np.arange(len(method))
plt.xticks(ypos, method)
plt.bar(ypos, et, 0.4, color=c)
plt.title("Time To Compute Primes")
plt.xlabel("Methods")
plt.ylabel("Elapsed Time (seconds)")
plt.show() 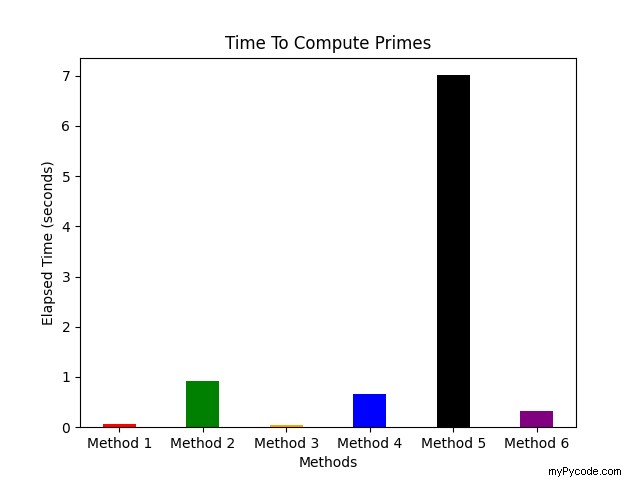
import plot
import matplotlib.pyplot as plt
import numpy as np
method = ['Method 1', 'Method 2', 'Method 3', 'Method 4', 'Method 5', 'Method 6']
et = [plot.m1_et, plot.m2_et, plot.m3_et, plot.m4_et, plot.m5_et, plot.m6_et]
ypos = np.arange(len(method))
plt.xticks(ypos, method)
plt.plot(ypos, et, color='green', linestyle='dashed', linewidth = 3,
marker='o', markerfacecolor='blue', markersize=12)
plt.title("Time To Compute Primes")
plt.xlabel("Methods")
plt.ylabel("Elapsed Time (seconds)")
plt.show() Conclusion