Cet article couvrira certaines fonctions mathématiques avancées fournies par Sympy bibliothèque. Si vous n'avez toujours pas lu le premier article d'introduction à Sympy, Vous pouvez le voir ici.
Étant donné que la plupart des fonctions de base, comme celles pour lancer un Sympy session sur votre terminal ou pour définir une fonction/variable, ne seront pas traités ici.
Dans cet article, nous allons explorer comment calculer les dérivées, les intégrales et les limites avec Sympy et aussi comment tracer des graphiques directement depuis la borne. Comme déjà dit dans l'article et la vidéo précédents, les commandes et fonctions qui seront décrites dans les sections suivantes peuvent être saisies à la fois dans le script et dans le terminal ; J'utiliserai le terminal car il offre une représentation des données plus intuitive et plus claire.
Nous commençons notre code en important le Sympy et Matplotlib bibliothèques; nous utiliserons cette dernière bibliothèque pour créer des tracés à partir de nos données. Si vous ne connaissez pas ou vous ne vous souvenez tout simplement pas de ces procédures, jetez un œil au premier article sur Sympy , où il est également décrit comment lancer un Sympy session et définissez les variables et les fonctions().
Dérivés et dérivés partiels
Le calcul des dérivées de fonctions mathématiques est une pratique très courante dans la plupart des domaines liés aux sciences; ce faisant, il est possible d'identifier l'emplacement des maxima et des minima d'une fonction, c'est-à-dire les points où elle commence à augmenter/diminuer.
Sympy permet de résoudre cette tâche de manière très immédiate ; la fonction utilisée à cet effet s'appelle diff(), de "différentiel". La fonction diff() , prend comme paramètre d'entrée la fonction que l'on veut dériver. Dans les lignes de code suivantes, nous définissons une fonction, "f", et nous calculons sa première dérivée.
>>> f = 3*x**2 + 4*x + 5 >>> diff(f) 6⋅x + 4
Comme vous avez pu le voir, en une seule ligne de code, nous avons réussi à calculer la dérivée de la fonction. Dans ce cas, il pourrait même être possible de calculer la dérivée seconde de "f" (il est plus correct de dire que dans ce cas la dérivée seconde n'est pas égale à zéro), puisqu'elle présente un terme du second ordre (x 2 ).
Pour calculer les dérivées secondes ou supérieures des fonctions avec Sympy, il suffit juste de préciser, après le nom de la fonction, la variable par rapport à laquelle on veut faire la dérivation et le nombre de fois qu'on veut faire la dérivation (i.e. calculer les dérivées). Dans les lignes de code suivantes, nous calculons la dérivée seconde de "f", c'est-à-dire que nous différencions la fonction deux fois.
>>> f
2
3⋅x + 4⋅x + 5
>>> diff(f, x, 2)
6
Dans ce cas également, Sympy rendu la tâche maladroitement facile et immédiate !
Lorsque nous avons affaire à des fonctions à plusieurs variables, nous pouvons être intéressés par le calcul de leurs dérivées partielles ; pour cela, il suffit de préciser la variable par rapport à laquelle on veut différencier la fonction. Dans l'exemple suivant, la fonction « g » est une fonction à trois variables (x, y, z); nous montrons donc comment calculer les dérivées partielles par rapport à chacune des trois variables.
>>> g = 2*x + 4*y**2 - x*z >>> diff(g, x) 2 - z >>> diff(g, y) 8⋅y >>> diff(g, z) -x
Intégrales
L'intégration est l'opération inverse par rapport à la différenciation. D'un point de vue graphique, intégrer une fonction signifie calculer l'aire entre la fonction et l'axe des abscisses, mais bien sûr, le potentiel du Calcul Intégral ne se limite pas aux zones sous les graphiques.
Dans cette section nous verrons premièrement comment exprimer une intégrale d'une fonction dans le terminal; comme vous le verrez, Sympy permet une meilleure représentation de la fonction au sein du terminal.
Pour cela, nous utilisons toujours la fonction "f" définie au début (vous pouvez la retrouver également dans les premières lignes de cette section de code) et nous définissons juste son intégrale, entre les points -2 et 2. Pour ce faire, on exploite la fonction Integral() et passer en paramètre d'entrée la fonction, la variable pour laquelle on veut intégrer, suivie des bornes inférieure et supérieure (ces trois derniers paramètres doivent être mis entre parenthèses).
>>> f 2 3⋅x + 4⋅x + 5 >>> Integral(f, (x, -2, 2)) 2 ⌠ ⎮ 2 ⎮ 3⋅x + 4⋅x + 5 dx ⌡ -2
A ce stade, nous venons d'exprimer l'intégrale que nous voulons résoudre, en utilisant la notation mathématique. Cependant, ce qui nous intéresse vraiment, c'est comment résoudre réellement l'intégrale. Pour résoudre l'intégrale, nous utilisons une fonction appelée integrate(); les paramètres d'entrée sont toujours les mêmes ; si vous souhaitez simplement résoudre l'intégrale symboliquement, vous n'avez pas à spécifier les limites d'intégration. Dans les lignes de code suivantes, nous résolvons d'abord l'intégrale symboliquement puis numériquement en saisissant tous les paramètres déjà utilisés avec la fonction Integral().
>>> integrate(f) 3 2 x + 2⋅x + 5⋅x >>> integrate(f, (x, -2, 2)) 36
Comme vous pouvez le voir, grâce à la fonction integrate() fonction, il était possible de résoudre l'intégrale à la fois symboliquement et numériquement d'une manière très immédiate. Avec une approche similaire, il est également possible de résoudre des intégrales doubles ou triples; il suffit de spécifier les bornes pour chaque variable, de la même manière que nous l'avons fait pour la variable x dans l'exemple ci-dessus ; dans les lignes de code suivantes, on calcule l'intégrale double de la fonction "g".
>>> g = x**2 + 5*y >>> integrate(g, (x, -2, 2), (y, 3, 5)) 512/3
Si on voulait résoudre symboliquement l'intégrale par rapport à une seule des deux variables, il aurait suffi de donner en entrée cette variable, juste après le nom de la fonction à intégrer ("g" dans ce cas).
Limites
En mathématiques, les limites sont utilisées pour évaluer une fonction lorsqu'elle s'approche de points "critiques" dans lesquels elle pourrait diverger ou converger vers des valeurs spécifiques, soit un nombre fini ou ± l'infini. Pour calculer les limites d'une fonction mathématique, on utilise le Sympy fonction limite(); il prend en entrée la fonction d'intérêt, la variable à laquelle la limite se réfère et le point auquel nous voulons calculer la limite, c'est-à-dire le point où la variable indépendante "s'approche". Dans l'exemple suivant, nous évaluons la limite de la fonction sin(x)/x lorsque x tend vers zéro.
>>> limit(sin(x)/x, x, 0) 1
Dans certains cas, les limites peuvent prendre des valeurs différentes selon que la variable indépendante s'approche du point critique à partir de valeurs supérieures ou inférieures ; un exemple est la limite de la fonction 1/x , évalué au voisinage de zéro ; comme vous le verrez, le résultat est différent si nous nous approchons de zéro à partir de nombres supérieurs ou inférieurs. Pour spécifier la direction à partir de laquelle nous voulons "approcher" le point critique, nous ajoutons un autre paramètre d'entrée, c'est-à-dire "-" ou "+", indiquant que nous approchons de ce point critique à partir de valeurs inférieures ou supérieures, respectivement.
>>> limit(1/x, x, 0, '-') -∞ >>> limit(1/x, x, 0, '+') ∞
Comme prévu, le résultat de la limite dans les deux cas varie de –∞ à +∞.
Fonctions de traçage
Dans cette dernière section, nous allons explorer une autre fonctionnalité très utile de Sympy, c'est la possibilité de tracer et donc d'afficher des fonctions en tapant simplement leurs équations, directement dans le terminal. Pour accomplir cette tâche, nous devrions avoir préalablement installé Matplotlib (à proprement parler, ce n'est pas obligatoire, Sympy est également capable de représenter l'ensemble de l'intrigue en utilisant des points et des lignes ; cependant, la sortie graphique n'est pas la meilleure; Je recommande personnellement d'installer et d'exploiter matplotlib). Dans les exemples suivants, nous ne verrons que quelques-unes des fonctions les plus importantes ; cependant, gardez à l'esprit qu'il existe de nombreuses autres possibilités et options différentes.
Si cela vous intéresse, consultez la documentation officielle ici :https://docs.sympy.org/latest/modules/plotting.html
Nous commençons par regarder comment tracer une seule fonction ; on affecte d'abord le tracé à la variable « p1 »; pour tracer la fonction, on utilise la fonction plot(), en saisissant comme paramètres d'entrée la fonction (exprimée explicitement) et les bornes de la variable indépendante (ce n'est pas obligatoire, si on ne précise pas de bornes, la fonction s'affichera de -5 à +5).
>>> p1 = plot(3*x + 4, (x, -3, 3))
À ce stade, nous devrions être en mesure de voir dans une fenêtre matplotlib séparée, le tracé de notre fonction ; La figure 1 présente le résultat de l'exemple.
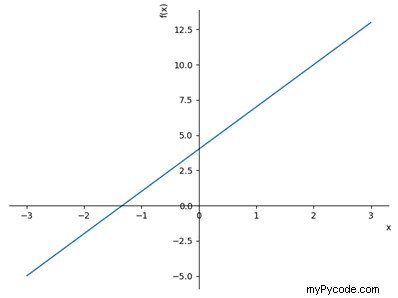
Illustration 1 : Tracé de la fonction f(x) =3x + 4, calculé pour les valeurs de x de -3 à +3.
Il est également possible de tracer plusieurs graphiques dans le même tracé, chacun d'eux avec ses propres limites ; pour cela, il suffit d'exploiter la fonction extend(). Dans les lignes de code suivantes, nous définissons un deuxième tracé, "p2", nous choisissons de ne pas l'afficher en spécifiant dans l'option "show=False" et via le extend() fonction, nous l'ajoutons au tracé initial, p1. On montre enfin p1. Le résultat final est affiché dans la figure 2.
>>> p2 = plot(x**2, (x, 3, 7), show=False) >>> p1.extend(p2) >>> p1.show()
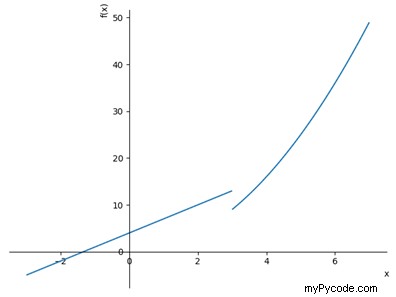
Illustration 2 : Le tracé "p2" (défini de x=3 à x=7) a été ajouté et affiché avec le tracé initial (p1).
Une autre fonctionnalité intéressante de Sympy est la possibilité de tracer des fonctions paramétriques comme les circonférences. Pour cela, nous pouvons exploiter la fonction plot_parametric(), ses paramètres d'entrée sont les coordonnées "x" et "y" des points définissant la courbe paramétrique, la variable paramétrique et ses frontières. Les lignes de code suivantes montrent comment tracer une circonférence centrée à l'origine des axes, avec sa variable indépendante variant de -7 à 7. La figure 3 affiche la fenêtre matplotlib avec le tracé ainsi généré.
>>> plot_parametric((cos(x), sin(x)), (x, -7, 7))
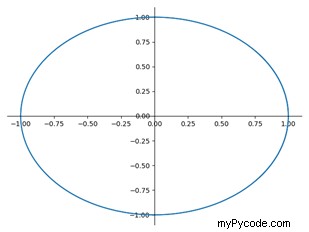
Figure 3 : Représentation paramétrique d'une circonférence centrée à l'origine des axes x et y.
La dernière fonction que nous allons explorer permet de tracer des fonctions donnant comme paramètre d'entrée l'équation sous forme implicite. Cette fonctionnalité pourrait être très utile lorsqu'il s'agit de fonctions vraiment complexes et longues, pour lesquelles il est souvent difficile d'obtenir la version explicite (c'est-à-dire celle dans laquelle une variable est exprimée en fonction de toutes les autres). Pour résoudre cette tâche, la fonction appropriée est plot_implicit(); les paramètres d'entrée sont la fonction implicite (c'est-à-dire celle qui affiche les deux variables dans son équation) et les bornes de chacune des variables. Dans les lignes de code suivantes, nous traçons une fonction parabolique, donnant en entrée son équation implicite et modifiant les limites des coordonnées x et y. Le résultat final est ensuite illustré à la figure 4.
>>> plot_implicit(x**2 + 2*y, (x, -2, 2), (y, -3, 3))
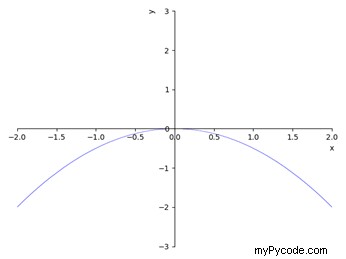
Illustration 4 : Tracé d'une fonction parabolique obtenu en passant en paramètre d'entrée son équation sous forme implicite.
Conclusion
Cet article a montré comment utiliser Sympy pour résoudre des tâches mathématiques telles que les dérivées, les intégrales et les limites. Dans la dernière partie, Sympy a été utilisé pour obtenir des tracés des fonctions directement à partir du terminal. Tout le code affiché dans les différentes sections a été saisi dans le terminal ; cependant, les mêmes résultats peuvent être obtenus en écrivant les mêmes fonctions dans le script. Ce n'était qu'une très brève introduction à l'incroyable capacité du Sympy bibliothèque, je vous suggère fortement de consulter la page de documentation officielle (https://www.sympy.org/en/index.html ), où vous trouverez une pléthore d'autres fonctions et options intéressantes qui pourraient immédiatement offrir une solution simple à la plupart de vos problèmes de maths.


