Problème :Comment calculer l'entropie avec la librairie SciPy ?
Solution :Importer le entropy() fonction du scipy.stats module et passez-y la probabilité et la base du logarithme.
from scipy.stats import entropy p = [0.5, 0.25, 0.125, 0.125] e = entropy(p, base=2) print(e) # 1.75
Essayez-le vous-même :Exécutez ce code dans le shell de code interactif !
Exercice :Modifier les probabilités. Comment l'entropie change-t-elle ?
Commençons doucement ! Vous apprendrez ensuite le contexte le plus pertinent sur l'entropie.
Introduction à l'entropie
En thermodynamique, l'entropie est expliquée comme un état d'incertitude ou aléatoire.
En statistique, on emprunte ce concept car il s'applique facilement au calcul des probabilités.
Lorsque nous calculons l'entropie statistique , nous quantifions la quantité d'informations dans un événement, une variable ou une distribution. Comprendre cette mesure est utile dans l'apprentissage automatique dans de nombreux cas, comme la création d'arbres de décision ou le choix du meilleur modèle de classificateur.
Nous discuterons des applications de l'entropie plus loin dans cet article, mais nous allons d'abord approfondir la théorie de l'entropie et comment la calculer avec l'utilisation de SciPy.
Calcul de l'entropie
Le calcul de l'information d'une variable a été développé par Claude Shannon , dont l'approche répond à la question, combien de questions "oui" ou "non" vous attendez-vous à poser pour obtenir la bonne réponse ?
Pensez à lancer une pièce. En supposant que la pièce est juste, vous avez 1 chance sur 2 de prédire le résultat. Vous devineriez pile ou face, et que vous ayez raison ou non, vous n'avez besoin que d'une seule question pour déterminer le résultat.
Maintenant, disons que nous avons un sac avec quatre disques de taille égale, mais chacun est d'une couleur différente :

Pour deviner quel disque a été tiré du sac, une des meilleures stratégies consiste à éliminer la moitié des couleurs. Par exemple, commencez par demander s'il est bleu ou rouge. Si la réponse est oui, alors une seule question supplémentaire est nécessaire puisque la réponse doit être bleue ou rouge. Si la réponse est non, alors vous pouvez supposer qu'il est vert ou gris, donc une seule question supplémentaire est nécessaire pour prédire correctement le résultat, ce qui porte notre total à deux questions, que la réponse à notre question soit vert ou gris.
Nous pouvons voir que lorsqu'un événement est moins susceptible de se produire, en choisissant 1 sur 4 par rapport à 1 sur 2, il y a plus d'informations à apprendre, c'est-à-dire deux questions nécessaires contre une.
Shannon a écrit son calcul de cette façon :
Information(x) = -log(p(x))
Dans cette formule log() est un algorithme de base 2 (car le résultat est vrai ou faux), et p(x) est la probabilité de x .
Plus la valeur de l'information augmente, moins le résultat devient prévisible.
Lorsqu'une probabilité est certaine (par exemple, un tirage au sort à deux faces qui tombe sur face), la probabilité est de 1,0, ce qui donne un calcul d'information de 0.
Nous pouvons exécuter le calcul de Shannon en python en utilisant le math bibliothèque affichée ici :
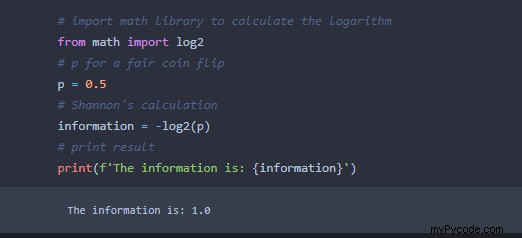
Lorsque nous modifions la probabilité à 0,25, comme dans le cas du choix de la bonne couleur du disque, nous obtenons ce résultat :
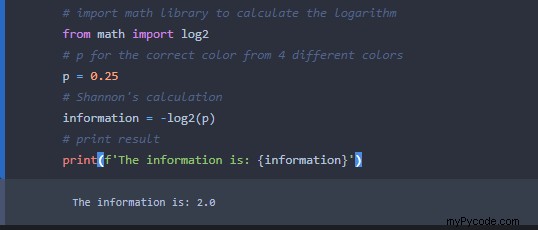
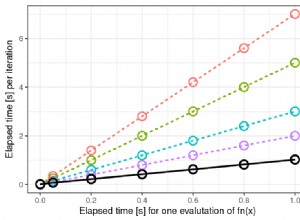
Bien qu'il semble que l'augmentation de l'information soit linéaire, que se passe-t-il lorsque nous calculons le résultat d'un seul dé ou demandons à quelqu'un de deviner un nombre entre 1 et 10 ? Voici un visuel des calculs d'information pour une liste de probabilités de moins certaine (p = 0.1 ) à certains (p = 1.0 ):
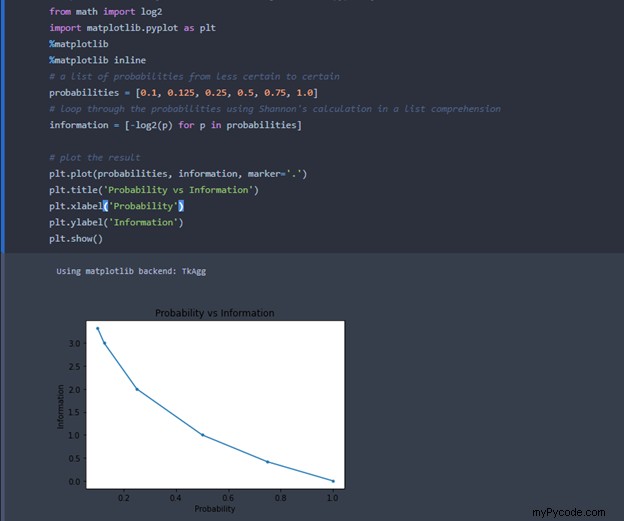
Le graphique montre qu'avec une plus grande incertitude, la croissance de l'information est sous-linéaire, et non linéaire.
Probabilités inégales
Pour en revenir à l'exemple des disques colorés, que se passe-t-il si nous avons maintenant 8 disques dans le sac et qu'ils ne sont pas également répartis ? Regardez cette répartition par couleur :
| Couleur | Quantité |
| Bleu | 1 |
| Vert | 1 |
| Rouge | 2 |
| Gris | 4 |
| Total | 8 |
Si nous utilisons la stratégie originale d'élimination de la moitié des couleurs en demandant si le disque est bleu ou vert, nous devenons moins efficaces car il y a une probabilité combinée de 0,25 que l'une ou l'autre des couleurs soit correcte dans ce scénario.
Nous savons que le gris a la probabilité la plus élevée. En utilisant une stratégie légèrement différente, nous demandons d'abord si Gray a raison (1 question), puis nous passons à la prochaine probabilité la plus élevée, Rouge (2 ème question), puis de vérifier si c'est Bleu ou Vert (3 rd questions).
Dans ce nouveau scénario, la pondération de nos suppositions conduira à moins d'informations requises. Les tableaux ci-dessous présentent la comparaison des deux méthodes. La colonne info est le produit des colonnes Probabilité et Questions.
| Conjectures égales | |||
| Couleur | Problème | Q's | Informations |
| Bleu | 0,25 | 2 | 0.50 |
| Vert | 0,25 | 2 | 0.50 |
| Rouge | 0,25 | 2 | 0.50 |
| Gris | 0,25 | 2 | 0.50 |
| Total | 1 | 8 | 2.00 |
| Conjectures pondérées | |||
| Couleur | Problème | Q's | Informations |
| Bleu | 0,125 | 3 | 0,375 |
| Vert | 0,125 | 3 | 0,375 |
| Rouge | 0,25 | 2 | 0.50 |
| Gris | 0.5 | 1 | 0.50 |
| Total | 1 | 9 | 1.75 |
La méthode d'estimation égale prend en moyenne 2 questions, mais la méthode d'estimation pondérée en prend en moyenne 1,75.
Nous pouvons utiliser la bibliothèque Scipy pour effectuer le calcul d'entropie. La sous-bibliothèque "stats" de Scipy a un calcul d'entropie que nous pouvons utiliser. Voici le code pour calculer l'entropie pour le scénario où les quatre disques ont des probabilités différentes :
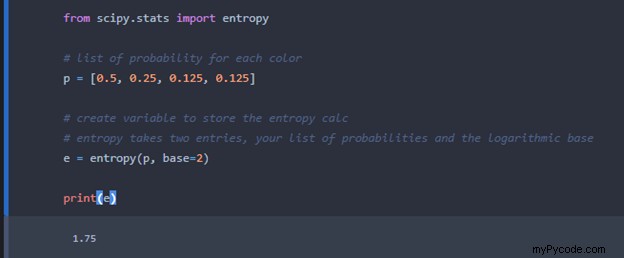
La méthode d'entropie prend deux entrées :la liste des probabilités et votre base. Base=2 est le choix ici puisque nous utilisons un log binaire pour le calcul.
Nous obtenons le même résultat que dans le tableau ci-dessus. Avec un minimum de code, la bibliothèque Scipy nous permet de calculer rapidement l'entropie de Shannon.
Autres utilisations
Le calcul d'entropie est utilisé avec succès dans l'application du monde réel dans l'apprentissage automatique. Voici quelques exemples.
Arbres de décision
Un arbre de décision est basé sur un ensemble de décisions binaires (vrai ou faux, oui ou non). Il est construit avec une série de nœuds où chaque nœud est question :Couleur ==bleu ? Le résultat du test est-il> 90 ? Chaque nœud se divise en deux et se décompose en sous-ensembles de plus en plus petits au fur et à mesure que vous vous déplacez dans l'arborescence.
La précision de votre arbre de décision est maximisée en réduisant votre perte. Utiliser l'entropie comme fonction de perte est un bon choix ici. A chaque étape se déplaçant à travers les branches, l'entropie est calculée avant et après chaque étape. Si l'entropie diminue, l'étape est validée. Sinon, vous devez essayer une autre branche.
Classification avec régression logistique
La clé d'une régression logistique consiste à minimiser la perte ou l'erreur pour obtenir le meilleur ajustement du modèle. L'entropie est la fonction de perte standard pour la régression logistique et les réseaux de neurones.
Exemple de code
Bien qu'il existe plusieurs choix pour utiliser l'entropie comme fonction de perte dans l'apprentissage automatique, voici un extrait de code pour montrer comment la sélection est effectuée lors de la compilation du modèle :

Conclusion
Le but de cet article était de faire la lumière sur l'utilisation de l'entropie avec Machine Learning et comment elle peut être calculée avec Python.