Cet article explore l'utilisation des fonctions .UnivariateSpline() et .LSQUnivariateSpline (), du paquet Scipy.
Que sont les splines ?
Les splines sont des fonctions mathématiques qui décrivent un ensemble de polynômes interconnectés en des points spécifiques appelés nœuds de la spline.
Ils sont utilisés pour interpoler un ensemble de points de données avec une fonction qui montre une continuité parmi la plage considérée ; cela signifie également que les splines généreront une fonction lisse, ce qui évite les changements brusques de pente.
Par rapport aux méthodes d'ajustement plus classiques, le principal avantage des splines est que l'équation polynomiale n'est pas la même sur toute la plage de points de données.
Au lieu de cela, la fonction d'ajustement peut changer d'un intervalle à l'autre, permettant l'ajustement et l'interpolation de distributions de points très compliquées. Dans cet article nous verrons :
- i) comment générer une fonction spline pour s'adapter un ensemble donné de points de données,
- ii) quelles fonctions nous pouvons ensuite utiliser pour extrapoler la valeur des points dans la plage ajustée,
- iii) comment améliorer le montage, et
- iv) comment calculer l'erreur associée .
Splines – Une perspective mathématique
En mathématiques, les splines sont des fonctions décrites par un ensemble de polynômes.
Même si les splines semblent être décrites par une seule équation, elles sont définies par différentes fonctions polynomiales qui s'appliquent sur une plage spécifique de points, dont les extrêmes sont appelés nœuds . Chaque nœud représente donc un changement dans la fonction polynomiale qui décrit la forme de la spline dans cet intervalle spécifique.
Une des principales caractéristiques des splines est leur continuité ; elles sont continues sur tout l'intervalle dans lequel elles sont définies; cela permet de générer une courbe lisse, qui correspond à notre ensemble de points de données.
L'un des principaux avantages d'utiliser des splines pour les problèmes d'ajustement, au lieu de polynômes simples, est la possibilité d'utiliser des fonctions polynomiales de degré inférieur pour décrire des fonctions très compliquées.
En effet, si l'on voulait utiliser une seule fonction polynomiale, le degré du polynôme augmente généralement avec la complexité de la fonction à décrire; augmenter le degré du polynôme d'ajustement pourrait introduire des erreurs indésirables dans le problème.
Voici une belle vidéo qui explique en termes simples ce problème :
Les splines évitent cela en faisant varier l'équation d'ajustement sur les différents intervalles qui caractérisent l'ensemble initial de points de données. D'un point de vue historique, le mot "Spline" vient des dispositifs de spline flexibles qui ont été exploités par les constructeurs navals pour dessiner des formes lisses dans la conception des navires. De nos jours, ils trouvent également une large application en tant qu'outils fondamentaux dans de nombreux logiciels de CAO (https://en.wikipedia.org/wiki/Spline_(mathematics)).
Scipy.UnivariateSpline
Dans la première partie de cet article, nous explorons la fonction .UnivariateSpline(); qui peut être utilisé pour ajuster une spline d'un degré spécifique à certains points de données.
Pour comprendre le fonctionnement de cette fonction, nous commençons par générer nos tableaux x et y initiaux de points de données. Le tableau x (appelé "x"), est défini en utilisant le np.linspace() fonction; le tableau y est défini en exploitant le np.random fonction appelée .randn() , qui renvoient un échantillon de la distribution normale standard.
Voir :https://numpy.org/devdocs/reference/random/generated/numpy.random.randn.html pour une documentation supplémentaire.
import matplotlib.pyplot as plt from scipy.interpolate import UnivariateSpline, LSQUnivariateSpline import numpy as np #x and y array definition (initial set of data points) x = np.linspace(0, 10, 30) y = np.sin(0.5*x)*np.sin(x*np.random.randn(30))
Une fois que nous avons défini l'ensemble initial de points de données, nous pouvons appeler la fonction .UnivariateSpline() , à partir du package Scipy et calculez la spline qui correspond le mieux à nos points.
Bien que la procédure soit assez simple, comprendre les paramètres fondamentaux qui définissent la fonction spline que nous voulons créer peut générer une certaine confusion ; pour cela, mieux vaut analyser en détail les principaux paramètres d'entrée pouvant être définis lors de l'appel de la fonction dans notre code.
Comme on peut également le voir dans la documentation (https://docs.scipy.org/doc/scipy/reference/generated/scipy.interpolate.UnivariateSpline.html), le .UnivariateSpline() La fonction accepte comme entrées obligatoires les tableaux x et y de points de données que nous voulons ajuster.
Dans la plupart des cas, notre but est d'adapter des fonctions compliquées et à cette fin, d'autres paramètres doivent être spécifiés.
L'un des paramètres les plus importants est "k", qui fait référence au degré des polynômes qui définissent les segments de spline. « k » peut varier entre un et cinq; augmenter le degré des polynômes permet un meilleur ajustement des fonctions plus compliquées; cependant, afin de ne pas introduire d'artefacts dans notre fit; la meilleure pratique consiste à utiliser le degré inférieur qui permet la meilleure procédure d'ajustement.
Un autre paramètre pertinent est "s", c'est un nombre flottant qui définit le soi-disant facteur de lissage , qui affecte directement le nombre de nœuds présents dans la spline. Plus précisément, une fois que nous fixons une valeur spécifique de "s", le nombre de nœuds sera augmenté jusqu'à ce que la différence entre la valeur des points de données d'origine dans le tableau y et leurs points de données respectifs le long de la spline soit inférieure à la valeur de " s » (voir documentation pour la formule mathématique). On peut comprendre que plus la valeur de "s" est faible, plus la précision d'ajustement et (la plupart du temps) le nombre de nœuds sont élevés, car nous demandons une plus petite différence entre les points d'origine et ceux ajustés.
Maintenant que les paramètres qui régissent la forme de notre spline sont plus clairs, nous pouvons revenir au code et définir la fonction spline. En particulier, nous donnerons comme tableaux d'entrée les tableaux « x » et « y » précédemment définis; la valeur du facteur de lissage est initialement fixée à cinq tandis que le paramètre "k" conserve la valeur par défaut, qui est de trois.
#spline definition spline = UnivariateSpline(x, y, s = 5)
La sortie de .UnivariateSpline() fonction est la fonction qui correspond à l'ensemble donné de points de données. À ce stade, nous pouvons générer un tableau x plus dense, appelé "x_spline" et évaluer les valeurs respectives sur l'axe y à l'aide de la fonction spline que nous venons de définir ; nous les stockons ensuite dans le tableau "y_spline" et générons le tracé.
x_spline = np.linspace(0, 10, 1000) y_spline = spline(x_spline) #Plotting fig = plt.figure() ax = fig.subplots() ax.scatter(x, y) ax.plot(x_spline, y_spline, 'g') plt.show()
Le résultat de cette procédure est affiché dans la figure 1.
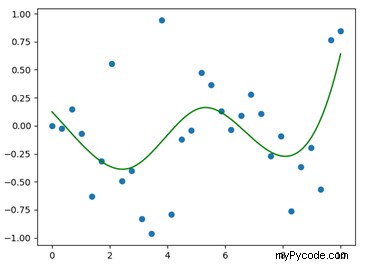
Comme on peut le voir sur la figure 1, la spline obtenue donne un très mauvais ajustement de nos points de données initiaux ; la raison principale est la valeur relativement élevée qui a été attribuée au facteur de lissage ; nous allons maintenant explorer une stratégie possible pour améliorer notre spline, sans introduire de modifications exagérées.
Une des meilleures manières d'améliorer cette situation est d'exploiter la méthode .set_smoothing_factor(s); qui continue le calcul de la spline selon un nouveau facteur de lissage (« s », donné comme seule entrée), sans altérer les nœuds déjà trouvés lors du dernier appel. Cela représente une stratégie pratique, en effet, les splines peuvent être très sensibles aux changements du facteur de lissage ; cela signifie que changer la fonction de lissage, directement dans le .UnivariateSpline() appelant, peut modifier de manière significative le résultat de sortie en termes de forme de spline (gardez à l'esprit que notre objectif est toujours d'obtenir le meilleur ajustement avec la spline la plus simple possible). Les lignes de code suivantes décrivent la définition d'une nouvelle fonction spline plus précise, avec un facteur de lissage égal à 0,5.
Après l'application de la méthode ci-dessus, la procédure est identique à celle décrite pour générer la première spline.
# Changing the smoothing factor for a better fit spline.set_smoothing_factor(0.05) y_spline2 = spline(x_spline)
Nous concluons en traçant le résultat; La figure 2 affiche la sortie finale, la nouvelle spline est la courbe bleue, tracée avec l'ancienne (courbe verte) et les points de données initiaux (points bleu clair).
#Plotting fig = plt.figure() ax = fig.subplots() ax.scatter(x, y) ax.plot(x_spline, y_spline, 'g', alpha =0.5) ax.plot(x_spline, y_spline2, 'b') plt.show()
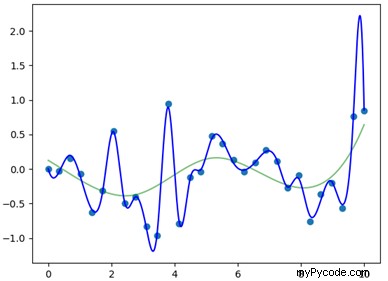
Comme on peut le voir sur la figure 2, la fonction spline nouvellement générée décrit bien les points de données initiaux et passe toujours par les nœuds qui ont été trouvés lors de l'appel initial (points de données communs aux deux fonctions spline)
Nous concluons cette partie en illustrant quelques méthodes utiles qui peuvent être utilisées après la génération de la fonction spline correcte, pour décrire nos points de données. La première de ces méthodes est appelée ".__call__(x)", qui permet d'évaluer la valeur de points spécifiques sur la spline, donnée sous la forme d'une liste ou d'un nombre unique. Les lignes suivantes décrivent l'application de cette méthode (on évalue la spline pour une valeur de 2 en abscisse).
#evaluate point along the spline print(spline.__call__(2))
Le résultat de la commande d'impression est 0,5029480519149454. Une autre méthode importante est .get_residual() , qui permet d'obtenir la somme pondérée des carrés des résidus de l'approximation spline (plus simplement, une évaluation de l'erreur dans la procédure d'ajustement).
#get the residuals print(spline.get_residual())
Le résultat pour ce cas est 0,049997585478530546. Dans certaines applications, il pourrait être intéressant de calculer l'intégrale définie de la spline (c'est-à-dire la zone sous la courbe de la spline entre une plage spécifique le long de l'axe des x); pour cela, la méthode .integral(a,b) représente la solution la plus simple ; « a » et « b » sont les limites inférieure et supérieure le long de l'axe des x entre lesquelles nous voulons évaluer la surface (dans ce cas, nous calculons la surface sous la spline, entre 1 et 2). L'application de cette méthode est illustrée dans les lignes suivantes.
#definite integral of the spline print(spline.integral(1,2))
Le résultat de l'intégration est -0,2935394976155577. La dernière méthode permet d'obtenir les valeurs des points où la spline croise l'axe des x, c'est-à-dire les solutions aux équations définissant la fonction spline. La méthode s'appelle .roots(), son application est illustrée dans les lignes suivantes.
#finding the roots of the spline function print(spline.roots())
La sortie de cette dernière ligne est un tableau contenant les valeurs des points pour lesquels la spline coupe l'axe des abscisses, à savoir :
[1.21877130e-03 3.90089909e-01 9.40446113e-01 1.82311679e+00 2.26648393e+00 3.59588983e+00 3.99603385e+00 4.84430942e+00 6.04000192e+00 6.29857365e+00 7.33532448e+00 9.54966590e+00]
Scipy.LSQUnivariateSpline
Dans la dernière partie de cet article, nous introduisons .LSQUnivariateSpline() , une autre fonction qui peut être utilisée pour la génération de splines. D'un point de vue pratique, cela fonctionne de la même manière que .UnivariateSpline() , en effet, comme nous le verrons, il y a très peu de différences dans la façon dont nous l'appelons et le définissons dans notre script.
La différence fondamentale entre cette fonction et la précédente, est que .LSQUnivariateSpline() permet de générer des courbes splines en contrôlant directement le nombre et la position des nœuds.
Cela signifie que nous avons le contrôle total des nœuds qui définira la spline ; différemment, dans le cas précédent, le nombre de nœuds était indirectement régulé par le choix du facteur de lissage. Afin d'apprécier comment notre spline va changer en augmentant le nombre de nœuds, nous commençons par définir deux tableaux différents, "t" et "t1", t1 est le tableau le plus dense.
#LSQUnivariateSpline t = np.array([0.5, 1, 2.5]) t1 = np.linspace(1, 9, 20)
La fonction .LSQUnivariateSpline () accepte en entrée obligatoire, les tableaux x, y et le tableau « t », qui contient les coordonnées des nœuds qui définiront notre spline. Une condition importante qui doit être gardée à l'esprit est que les coordonnées des nœuds doivent être situées dans la plage du tableau x.
Dans notre cas, nous utiliserons les mêmes tableaux x et y employés pour le cas précédent. À ce stade, nous devons appeler la fonction deux fois, afin de montrer la différence entre les deux ensembles de tableaux de nœuds. De plus, nous spécifions le paramètre "k", qui fait à nouveau référence au degré des polynômes qui décrivent la spline.
LSQUspline = LSQUnivariateSpline(x, y, t1, k = 4) LSQUspline1 = LSQUnivariateSpline(x, y, t, k = 4)
Notre dernière tâche consiste à tracer les deux splines, ainsi que les points de données d'origine. Nous allons générer les tableaux contenant les valeurs y des deux splines directement dans la commande de tracé.
#Plotting plt.scatter(x, y, s=8) plt.plot(x_spline, LSQUspline(x_spline), color = 'b') plt.plot(x_spline, LSQUspline1(x_spline), color = 'g') plt.show()
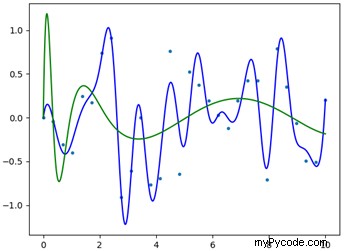
Le résultat final est affiché sur la figure 3; comme on peut le voir, en augmentant le nombre de nœuds, la fonction spline se rapproche mieux de nos points de données. Si nous vérifions attentivement, les deux splines passent pour les nœuds spécifiés dans les tableaux "t" et "t1", respectivement. La plupart des méthodes présentées précédemment pour .UnivariateSpline() travaillez également sur cette fonction (pour une documentation supplémentaire, veuillez vous référer à https://docs.scipy.org/doc/scipy/reference/generated/scipy.interpolate.LSQUnivariateSpline.html ).
Conclusion
Pour conclure, dans cet article, nous avons exploré les fonctions splines, leur puissance et leur polyvalence.
Une chose qu'il est important de garder à l'esprit est que lorsque nous utilisons des splines pour ajuster et interpoler un ensemble donné de points de données, nous ne devons jamais dépasser le degré des polynômes qui définissent la spline ; ceci afin d'éviter des erreurs indésirables et une interprétation incorrecte des données initiales.
Le processus doit être affiné avec précision, éventuellement par des itérations répétitives pour vérifier la validité de la sortie générée.